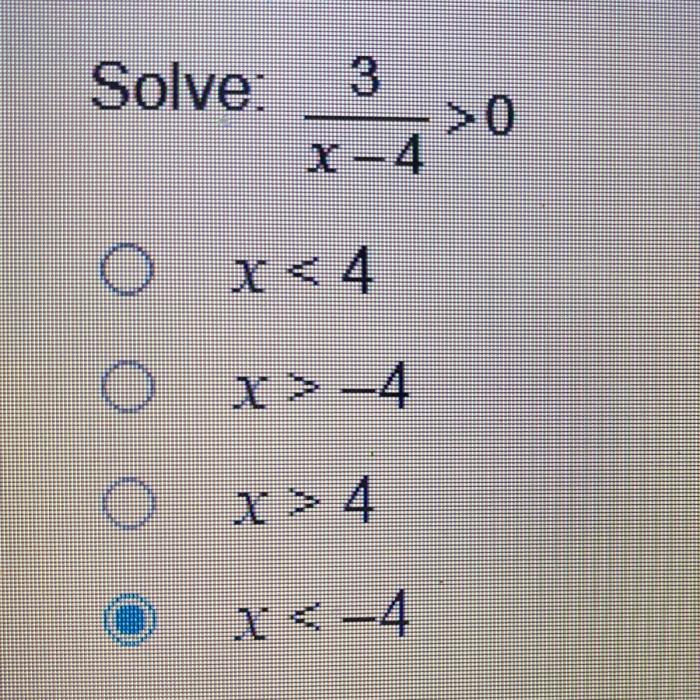What is the solution set of the quadratic inequality mc010-1.jpg – What is the solution set of a quadratic inequality? A quadratic inequality is an inequality that can be written in the form ax^2 + bx + c > 0 or ax^2 + bx + c< 0, where a, b, and c are real numbers and a ≠ 0. The solution set of a quadratic inequality is the set of all values of x that make the inequality true.
Quadratic inequalities are commonly used in various fields such as mathematics, physics, and engineering. They can be used to model real-world problems such as finding the range of values for which a function is positive or negative, or finding the critical points of a function.
Solution Set of Quadratic Inequalities

Quadratic inequalities are a powerful tool for solving problems in a wide variety of fields, including mathematics, physics, and engineering. In this article, we will explore the concept of quadratic inequalities, their solution sets, and how to solve them using various methods.
Solution Set Definition
The solution set of an inequality is the set of all values of the variable that make the inequality true. For example, the solution set of the inequality x > 5 is the set of all numbers greater than 5.
Quadratic Inequality
A quadratic inequality is an inequality that can be written in the form ax^2 + bx + c > 0 or ax^2 + bx + c< 0, where a, b, and c are constants and a ≠ 0.
Solution Set of a Quadratic Inequality
To find the solution set of a quadratic inequality, we can use the following steps:
- Factor the quadratic expression on the left-hand side of the inequality.
- Set each factor equal to zero and solve for x.
- Plot the solutions on a number line.
- Determine the intervals where the inequality is true.
Graphical Representation
We can also solve quadratic inequalities graphically by graphing the quadratic function on the left-hand side of the inequality. The solution set is the set of all values of x for which the graph is above (for >) or below (for<) the x-axis.
Examples and Applications, What is the solution set of the quadratic inequality mc010-1.jpg
Quadratic inequalities have a wide range of applications in various fields, including:
- Mathematics: Solving equations, finding roots of polynomials
- Physics: Describing projectile motion, calculating acceleration
- Engineering: Designing structures, optimizing systems
Essential Questionnaire: What Is The Solution Set Of The Quadratic Inequality Mc010-1.jpg
What is the difference between a quadratic equation and a quadratic inequality?
A quadratic equation is an equation that can be written in the form ax^2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. A quadratic inequality is an inequality that can be written in the form ax^2 + bx + c > 0 or ax^2 + bx + c< 0, where a, b, and c are real numbers and a ≠ 0.
How do I solve a quadratic inequality?
There are several methods that can be used to solve a quadratic inequality. One common method is to use the quadratic formula. Another method is to graph the quadratic inequality and find the values of x that make the inequality true.
What are some applications of quadratic inequalities?
Quadratic inequalities are used in various fields such as mathematics, physics, and engineering. They can be used to model real-world problems such as finding the range of values for which a function is positive or negative, or finding the critical points of a function.