Embark on an intellectual journey with the Half Life Graph Worksheet Answer Key, a comprehensive guide that unlocks the secrets of scientific decay. Delve into the intricacies of half-life, unraveling its mathematical representation and practical applications in diverse fields.
Unveiling the mysteries of half-life graphs, this guide meticulously examines their structure and interpretation, empowering you with the ability to decipher their slopes and intercepts. Through engaging problem-solving techniques, you will master the art of half-life calculations, avoiding common pitfalls and misconceptions.
Half-Life Concept and Mathematical Representation
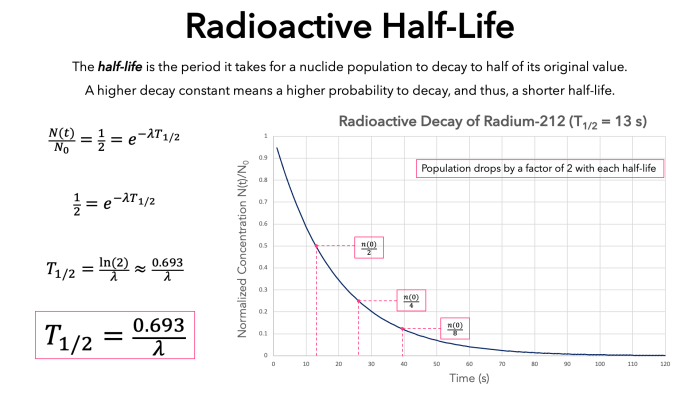
The concept of half-life is a fundamental aspect of radioactive decay and other exponential decay processes. It refers to the time required for half of a given quantity of a substance to undergo a specific transformation or decay.
In scientific terms, half-life is mathematically represented by the following equation:
t1/2= (ln 2) / λ
where:
- t 1/2is the half-life
- ln 2 is the natural logarithm of 2 (approximately 0.693)
- λ is the decay constant, which represents the rate of decay of the substance
The relationship between half-life and decay rate is inverse. A shorter half-life indicates a faster decay rate, while a longer half-life corresponds to a slower decay rate.
Half-Life Graph
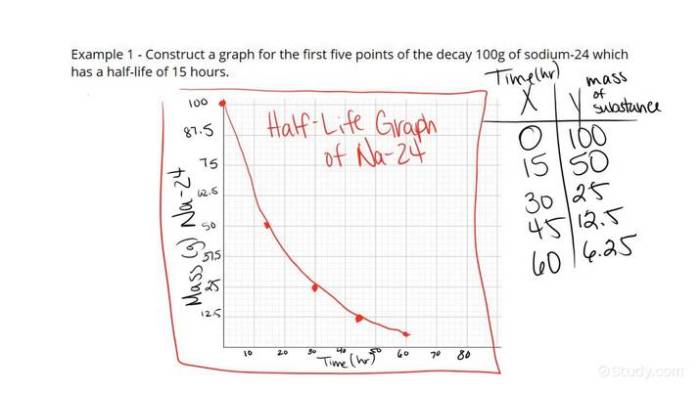
A half-life graph is a graphical representation of the decay of a substance over time. It is a plot of the amount of substance remaining versus time.
The graph is typically a smooth, exponential curve that decreases over time. The shape of the curve is determined by the half-life of the substance, which is the amount of time it takes for half of the substance to decay.
Structure of a Half-Life Graph
A half-life graph has two labeled axes: the x-axis, which represents time, and the y-axis, which represents the amount of substance remaining.
The units on the x-axis are typically minutes, hours, days, or years, depending on the half-life of the substance. The units on the y-axis are typically moles, grams, or counts, depending on the nature of the substance.
Interpretation of a Half-Life Graph
The slope of the half-life graph is equal to the negative of the rate constant for the decay process. The rate constant is a measure of how quickly the substance decays.
The intercept of the half-life graph is equal to the initial amount of substance present.
By analyzing the slope and intercept of the graph, it is possible to determine the half-life of the substance and the rate at which it decays.
Half-Life Worksheet
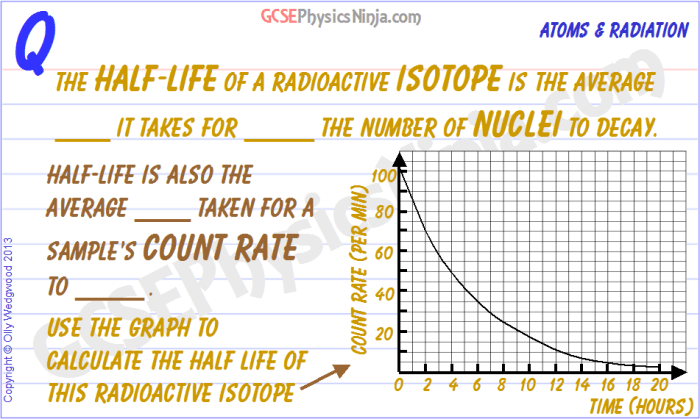
This worksheet provides practice problems to enhance understanding of half-life concepts and their graphical representation. By working through these problems, students can develop proficiency in solving half-life problems and avoid common pitfalls.
To solve half-life problems using a graph, follow these steps:
- Identify the half-life value (t1/2) from the graph.
- Determine the initial amount (N 0) of the substance.
- Count the number of half-lives (n) that have elapsed from the initial time.
- Calculate the amount (N) remaining after n half-lives using the formula: N = N 0
(1/2)n.
Common mistakes to avoid include:
- Misinterpreting the half-life value on the graph.
- Incorrectly counting the number of half-lives.
- Using the wrong formula to calculate the remaining amount.
Applications of Half-Life Graphs: Half Life Graph Worksheet Answer Key
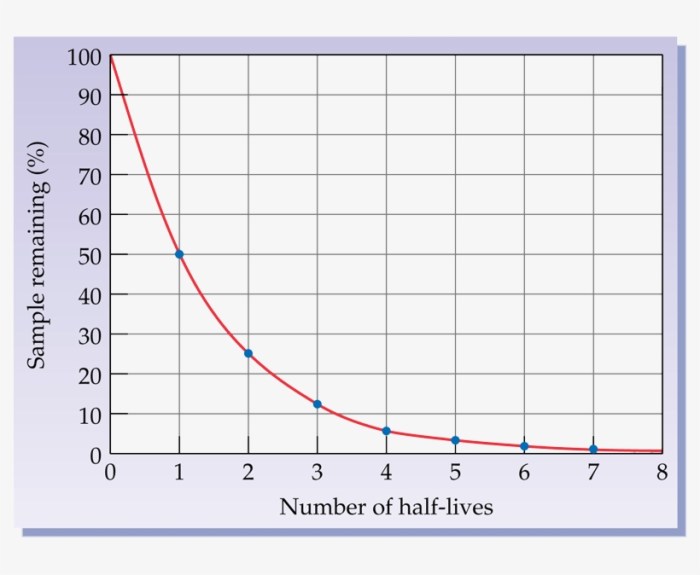
Half-life graphs are essential tools in various scientific disciplines, providing valuable insights into processes involving exponential decay. These graphs enable scientists and researchers to analyze and predict the behavior of substances or phenomena that undergo a gradual decrease over time.
Medicine
- Pharmacokinetics:Half-life graphs help determine the rate at which drugs are absorbed, distributed, metabolized, and excreted from the body. This information is crucial for optimizing drug dosage and treatment plans.
- Radioactive Isotopes:Half-life graphs are used to monitor the decay of radioactive isotopes used in medical imaging and therapy. By understanding the half-life of a specific isotope, medical professionals can calculate the optimal dosage and exposure time.
Chemistry
- Radioactive Decay:Half-life graphs are fundamental in studying the decay of radioactive elements. They allow scientists to determine the rate of decay and predict the amount of radioactive material remaining at a given time.
- Chemical Reactions:Half-life graphs can be used to analyze the progress of chemical reactions. By plotting the concentration of reactants or products over time, scientists can determine the rate of reaction and identify the half-life of the reaction.
Environmental Science
- Radioactive Waste Management:Half-life graphs are crucial for determining the storage and disposal requirements of radioactive waste. By understanding the half-life of radioactive isotopes, scientists can estimate the time it takes for the waste to decay to safe levels.
- Environmental Remediation:Half-life graphs are used to track the degradation of pollutants in the environment. This information helps scientists assess the effectiveness of remediation efforts and predict the time it will take for contaminants to reach acceptable levels.
Half-Life Answer Key
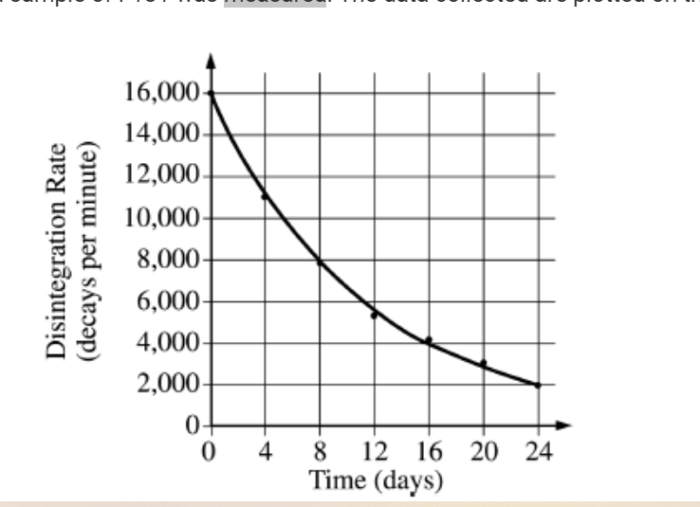
The half-life answer key provides accurate solutions and explanations for the half-life worksheet problems. It addresses common pitfalls and misconceptions associated with half-life calculations.
Answer Key, Half life graph worksheet answer key
- Problem 1:A radioactive isotope has a half-life of 10 hours. If you start with 100 grams of the isotope, how much will remain after 30 hours?
Answer:12.5 grams
Explanation:After 10 hours, 50 grams remain (half-life). After 20 hours, 25 grams remain (half of the remaining 50 grams). After 30 hours, 12.5 grams remain (half of the remaining 25 grams).
- Problem 2:The half-life of carbon-14 is 5,730 years. If an artifact contains 10% of its original carbon-14, how old is it?
Answer:34,380 years
Explanation:After one half-life, 50% of the original carbon-14 remains. After two half-lives, 25% remains. After three half-lives, 12.5% remains. After four half-lives, 6.25% remains. Since the artifact contains 10% of its original carbon-14, it has undergone four half-lives.
Therefore, its age is 4 x 5,730 years = 34,380 years.
Query Resolution
What is the concept of half-life?
Half-life represents the time it takes for a substance to decay to half of its original amount.
How is half-life represented mathematically?
Half-life can be represented by the equation: t1/2 = (ln 2) / k, where t1/2 is the half-life, ln is the natural logarithm, and k is the decay rate.
What is the relationship between half-life and decay rate?
Half-life is inversely proportional to decay rate. A shorter half-life indicates a faster decay rate.